分析地震目录#

  • 本节贡献者: 田冬冬（作者）、姚家园（审稿）

  • 最近更新日期: 2022-07-31

  • 预计花费时间: 15 分钟

在获取地震目录之后，通常还需要对地震目录做一些简单的绘图和分析。这一节演示如何 绘制最简单的地震深度直方图、地震震级直方图以及震级-频次关系图。

首先，需要把地震目录准备好。这里我们选择下载 2000–2010 年间震级大于 4.8 级， 震源深度大于 50 km 的地震。这一地震目录中共计约 7000 个地震：

from obspy.clients.fdsn import Client

client = Client("USGS")
cat = client.get_events(
    starttime="2000-01-01",
    endtime="2010-01-01",
    minmagnitude=4.8,
    mindepth=50,
)
print(cat)

6980 Event(s) in Catalog:
2009-12-31T17:42:15.960000Z | -19.747, -177.753 | 5.4  mwc | manual
2009-12-31T09:06:01.250000Z |  -7.499, +127.930 | 5.1  mb | manual
...
2000-01-02T12:14:39.090000Z | -17.943, -178.476 | 5.5  mwc | manual
2000-01-01T05:24:35.290000Z | +36.874,  +69.947 | 5.1  mwc | manual
To see all events call 'print(CatalogObject.__str__(print_all=True))'

为了进一步对数据做处理以及绘图，我们还需要导入 NumPy 和 Matplotlib 模块：

import matplotlib.pyplot as plt
import numpy as np

地震深度分布直方图#

为了绘制地震深度直方图，我们先从地震目录中提取出地震深度信息，并保存到数组 depth 中。 需要注意的是，ObsPy 的地震目录中地震深度的单位为 m，所以需要除以 1000.0 将深度单位 转换为 km。

depth = np.array([event.origins[0].depth / 1000 for event in cat])

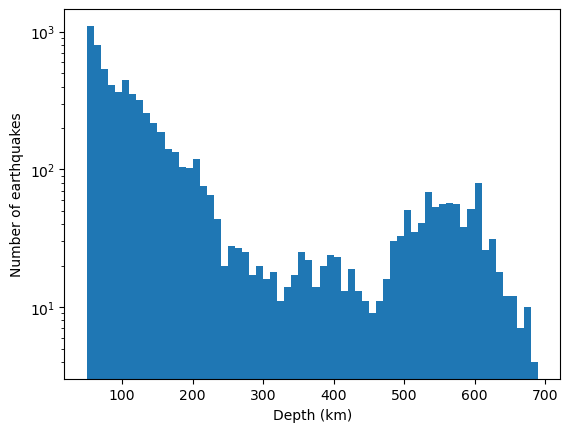
我们可以使用 Matplotlib 的 hist() 函数绘制直方图： 这里我们设置的直方的最小值为 50，最大值 700，间隔为 10，同时设置了 Y 轴以对数方式显示。 从图中可以明显看到地震深度随着深度的变化：

fig, ax = plt.subplots()
ax.hist(depth, bins=np.arange(50, 700, 10), log=True)
ax.set_xlabel("Depth (km)")
ax.set_ylabel("Number of earthquakes")
plt.show()
../../_images/catalog-analysis_7_0.png

地震震级直方图#

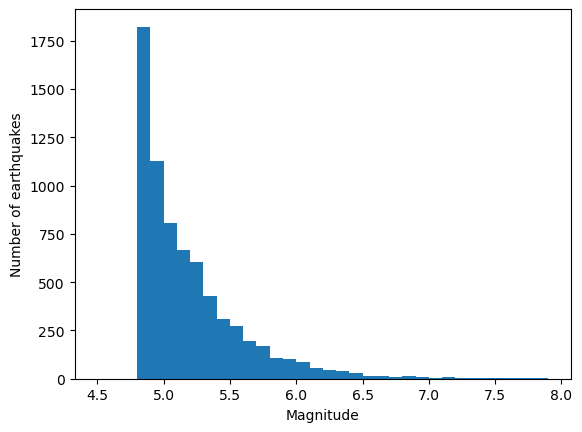
同理，从地震目录中提取出地震震级信息，保存到数组 mag 中并绘图。从图中可以明显看到， 震级越小地震数目越多：

mag = np.array([event.magnitudes[0].mag for event in cat])

fig, ax = plt.subplots()
ax.hist(mag, bins=np.arange(4.5, 8, 0.1))
ax.set_xlabel("Magnitude")
ax.set_ylabel("Number of earthquakes")
plt.show()
../../_images/catalog-analysis_9_0.png

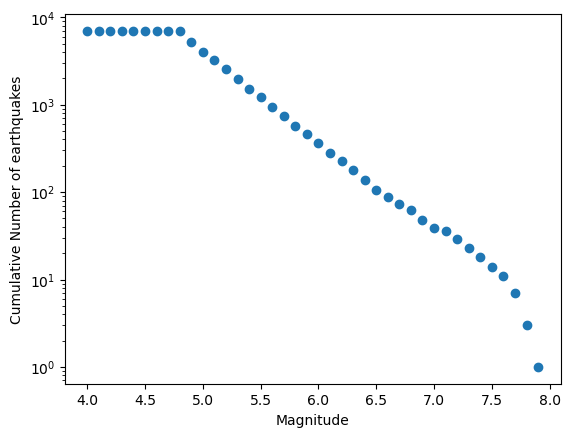
地震震级-频度关系#

地震震级-频度关系应符合 Gutenberg–Richter 定律。为了绘制地震震级-频度关系， 首先需要计算得到 GR 定律里的 \(N\)，即大于等于某个特定震级 \(M\) 的地震数目。 这里，我们选择 \(M\) 的取值范围为 4.0 到 8.0，间隔为 0.1。计算 \(N\) 的方法有很多，下面的 方法使用了 Python 的列表表达式以及 numpy.sum() 函数来实现：

mw = np.arange(4.0, 8.0, 0.1)
counts = np.array([(mag >= m).sum() for m in mw])

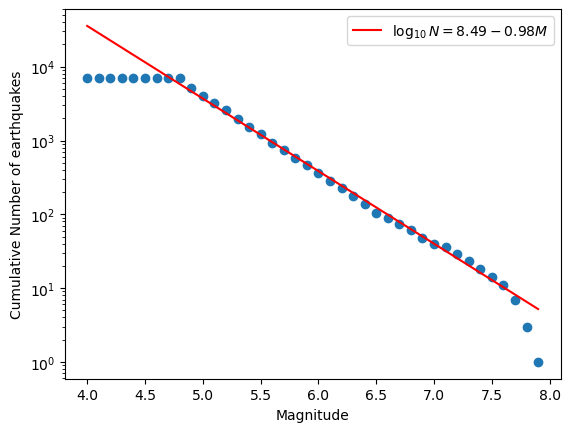
绘图脚本如下，注意图中 Y 轴是对数坐标。从图中可以明显看到 \(\log_{10}N\) 与 \(M\) 在 4.8 - 7.6 级 之间存在线性关系。由于我们使用的地震目录里只有 4.8 级以上的地震，所以在 4.7 级以下偏离了线性关系，而大地震由于数目太少也偏离了线性关系。

fig, ax = plt.subplots()
ax.semilogy(mw, counts, "o")
ax.set_xlabel("Magnitude")
ax.set_ylabel("Cumulative Number of earthquakes")
plt.show()
../../_images/catalog-analysis_13_0.png

更进一步，我们可以对 4.8-7.6 级之间的数据进行线性拟合，得到 GR 定律中的系数 \(a\) 和 \(b\)。 这里我们采用 numpy.logical_and 函数找到数组 mw 中所有满足条件的元素的索引， 并使用 NumPy 的布尔索引功能筛选出满足条件的震级 mw[idx] 和对应的 counts[idx]，再 使用 numpy.polyfit() 函数拟合一元一次多项式，最后绘图：

idx = np.logical_and(mw >= 4.8, mw <= 7.5)
# fitting y = p[0] * x + p[1]
p = np.polyfit(mw[idx], np.log10(counts[idx]), 1)
N_pred = 10 ** (mw * p[0] + p[1])

fig, ax = plt.subplots()
ax.semilogy(mw, counts, "o")
ax.semilogy(mw, N_pred, color="red", label=f"$\log_{{10}} N={p[1]:.2f}{p[0]:.2f}M$")
ax.legend()
ax.set_xlabel("Magnitude")
ax.set_ylabel("Cumulative Number of earthquakes")
plt.show()
../../_images/catalog-analysis_15_0.png